Unity 外接円の接線を求める

垂線を利用して三角形の外接円の接線を求める方法をメモメモ…

※このページの内容の動作確認にはUnity2018.2を使用しています。

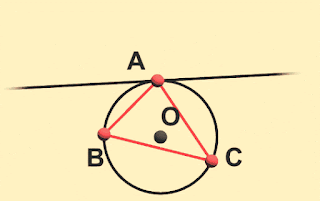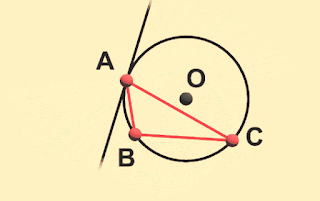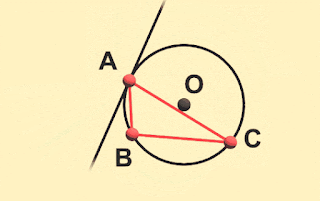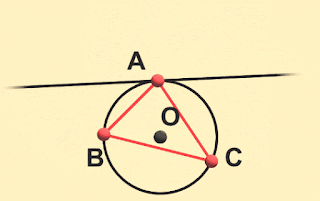
前回の投稿では垂線の足の座標を計算する方法について調べました。今回はその方法を使って三角形の頂点における外接円の接線を求めてみたいと思います。たとえば三角形ABCの頂点Aにおける外接円の接線は、下の図の赤いラインです。

外接円の接線を取得する

Wikipedia の Altitude のページにある Orthic triangle のセクションには次のような記述があります。

The sides of the orthic triangle are parallel to the tangents to the circumcircle at the original triangle's vertices.

「垂足三角形の辺(たとえば図のDE)は、もとの三角形の頂点(たとえば頂点A)の外接円の接線に平行である」ということです。つまり、 頂点Bと頂点Cから下ろした垂線の足を結べば、求めたい直線の向きがわかるということですね。たぶんもっと簡単な方法もあるとは思いますが、とりあえず今回はこの性質を利用しましょう。

public Vector3 a;
public Vector3 b;
public Vector3 c;

void Update ()
{
 // 三角形ABCの頂点Aにおける外接円の接線を計算する
 Vector3 d = PerpendicularFootPoint(a, c, b);
 Vector3 e = PerpendicularFootPoint(a, b, c);
 Vector3 tan = (e - d).normalized;
 Vector3 tangenttoB = a + tan;
 Vector3 tangenttoC = a - tan;
}

// 点Pから直線ABに下ろした垂線の足の座標を返す
Vector3 PerpendicularFootPoint(Vector3 a, Vector3 b, Vector3 p)
{
 return a + Vector3.Project(p - a, b - a);
}

で、この外接円の接線に一体どんな使い道があるかというと、たとえばベジェ曲線を使って頂点をなめらかにすることができたりします。

接線さえわかればベジェ曲線が使える

あんまり綺麗なコードじゃないですが参考までに自作のものを載せておきます。

public Vector3 a;
public Vector3 b;
public Vector3 c;
public float roundness;
public int maxWaypoints;

Vector3[] waypointsAB, waypointsAC;
 
void Update()
{
 float distAB = Vector3.Distance(a, b);
 float distAC = Vector3.Distance(a, c);

 // 三角形ABCの頂点Aにおける外接円の接線を計算する
 Vector3 d = PerpendicularFootPoint(a, c, b);
 Vector3 e = PerpendicularFootPoint(a, b, c);
 Vector3 tan = (e - d).normalized;
 if (tan == Vector3.zero) tan = (c - b).normalized;
 tan = tan * Mathf.Max(0, roundness);
 if (Vector3.Dot(b - a, c - a) > 0) tan = -tan;
 Vector3 tangenttoB = a - tan * distAB;
 Vector3 tangenttoC = a + tan * distAC;

 // ベジェ曲線を使って補間する
 waypointsAB = new Vector3[maxWaypoints];
 waypointsAC = new Vector3[maxWaypoints];
 for (int i = 0; i < maxWaypoints; i++)
 {
  float t = 1f / (maxWaypoints + 1) * (i + 1);
  waypointsAB[i] = QuadraticBezierPoint(a, b, tangenttoB, t);
  waypointsAC[i] = QuadraticBezierPoint(a, c, tangenttoC, t);
 }
}

// 点Pから直線ABに下ろした垂線の足の座標を返す
Vector3 PerpendicularFootPoint(Vector3 a, Vector3 b, Vector3 p)
{
 return a + Vector3.Project(p - a, b - a);
}

// 2次ベジェ曲線上の点を返す
Vector3 QuadraticBezierPoint(Vector3 start, Vector3 end, Vector3 tangent, float t)
{
 t = Mathf.Clamp01(t);
 float u = 1f - t;
 return u * u * start + 2f * u * t * tangent + t * t * end;
}

もしも ∠A=90° だった場合は点Dと点Eが重なるため、接線が零ベクトルになってしまいます。そうなるとベジェ曲線が機能しなくなってマズいので、その場合は一応ベクトルBCで代用しています(18行目)。それから頂点の位置関係によっては接線のベクトルの向きが逆になって曲線がねじれたりする可能性があるので、内積を使ってチェックし、ひっくり返すようにしています(20行目)。また上の例では2次のベジェ曲線を使っていますが、もちろん3次ベジェ曲線でもOKです。

外接円の中心を取得する

今回は垂線の足を利用して外接円の接線のベクトルを直接求めましたが、もし外接円の中心(外心)の座標を求めたいという場合は、もう少し手間がかかるかもしれません。外心の座標は「2つの辺のそれぞれの中点から垂直に伸ばした線の交点」と同じなので、素直に計算すると

辺の中点を求める
辺に直行するベクトルを求める
2つのベクトルの交点を求める

という処理が必要になります。このうちベクトルの交点座標は次のようなコードで計算することができます。

// 2つの直線の交点を返す
// http://wiki.unity3d.com/index.php/3d_Math_functions より一部改変
Vector3 LineLineIntersection(Vector3 linePoint1, Vector3 lineVec1, Vector3 linePoint2, Vector3 lineVec2)
{ 
 Vector3 lineVec3 = linePoint2 - linePoint1;
 Vector3 crossVec1and2 = Vector3.Cross(lineVec1, lineVec2);
 Vector3 crossVec3and2 = Vector3.Cross(lineVec3, lineVec2);
 
 float planarFactor = Vector3.Dot(lineVec3, crossVec1and2);
 
 // 直線がねじれの位置にある場合 or 平行な場合は零ベクトルを返す
 if(Mathf.Abs(planarFactor) < 0.0001f && crossVec1and2.sqrMagnitude > 0.0001f)
 {
  float s = Vector3.Dot(crossVec3and2, crossVec1and2) / crossVec1and2.sqrMagnitude;
  return linePoint1 + (lineVec1 * s);
 }
 else
 {
  return Vector3.zero;
 }
}

もしかしたらもっと効率的な方法があるかもしれませんが、こういう幾何学の分野についてはせいぜい高校レベルまでの知識しか持ち合わせていないので、正直よく分かりません…。まあ、とにかく狙い通りの実装はできたのでこれでよしとします。

なにはともあれ外接円の中心(外心)と接線は計算できた！

もう少し具体的なコードが知りたい！という方は次のページを参考にしてください。

おねむゲーマーの備忘録

2019年3月29日