Unityでメッシュ上にあるランダムな点を取得する方法をメモメモ…
※このページの内容の動作確認にはUnity2018.2を使用しています。
メッシュ表面のランダムな座標を計算する 前編前回はメッシュデータの中から三角面をランダムに取得する方法を考えました。三角形の面積に応じて「重み」がつくように Walker's Alias Method というアルゴリズムを利用してみたのですが、思いのほか長くなってしまったので今回はその続きからです。とはいっても三角面さえ選んでしまえばあとはその内部にある座標を計算すればいいだけなので残りはそんなに難しくありません。
三角形の内部にあるランダムな点を取得する
三角面の内側にある座標を算出する方法はこちらのページを参考にしました。三角形の各頂点の位置がわかれば、ランダムな座標は次のように求められます。Vector3 RandomPointInsideTriangle(Vector3 p1, Vector3 p2, Vector3 p3)
{
float a = Random.value;
float b = Random.value;
if (a + b > 1f)
{
a = 1f - a;
b = 1f - b;
}
float c = 1f - a - b;
return a * p1 + b * p2 + c * p3;
}
高校の数Bで習う「空間ベクトルの点の存在範囲」という内容です。さっぱり忘れてたのでググりましたが、ぶっちゃけ習ったかどうかすら怪しい…。まあそれはさておき OP = sOA + tOB + uOC という関係性のベクトルがあった場合、点Pが△ABC内に存在するための条件は
- s + t + u = 1
- s ≧ 0, t ≧ 0, u ≧ 0
では、この RandomPointInsideTriangle メソッドを使って座標を計算してみましょう。
// 各三角形の面積を考慮しつつランダムなインデックスを取得 int randomIndex = weightedRandom.GetRandomIndex(); // 選択した三角形の内部にあるランダムな座標を計算 Vector3 p1 = vertices[triangles[randomIndex*3]]; Vector3 p2 = vertices[triangles[randomIndex*3+1]]; Vector3 p3 = vertices[triangles[randomIndex*3+2]]; Vector3 pos = RandomPointInsideTriangle(p1, p2, p3); // グローバル座標に変換 pos = transform.TransformPoint(pos);
取得した座標(p1, p2, p3)はメッシュデータの内部の座標なので、実際にUnityで使用する場合は11行目のようにワールド空間へ変換しておくと便利だと思います。
メッシュの表面にオブジェクトを生成する
それではこれまで紹介してきた内容を踏まえて、実際に「スペースキーを押すたびにメッシュ表面のランダムな地点にオブジェクトを生成する」というスクリプトを書いてみましょう。using UnityEngine;
[RequireComponent(typeof(MeshFilter))]
public class RandomSpawnOnMesh : MonoBehaviour {
public GameObject spawnObject;
MeshFilter meshFilter;
Vector3[] vertices;
Vector3[] normals;
int[] triangles;
WeightedRandom weightedRandom;
void Start ()
{
meshFilter = GetComponent<MeshFilter>();
Mesh mesh = meshFilter.sharedMesh;
if (mesh == null) return;
// メッシュの各情報を取得しておく
vertices = mesh.vertices;
triangles = mesh.triangles;
normals = mesh.normals;
int trisNum = triangles.Length / 3;
// すべての三角形の面積を計算
float[] areas = new float[trisNum];
Vector3 p1, p2, p3;
for (int i = 0; i < trisNum; i++)
{
p1 = vertices[triangles[i*3]];
p2 = vertices[triangles[i*3+1]];
p3 = vertices[triangles[i*3+2]];
areas[i] = Vector3.Cross(p1 - p2, p1 - p3).magnitude;
}
// ランダム抽選用オブジェクトを準備
weightedRandom = new WeightedRandom(areas);
}
void Update ()
{
// スペースキーが押されたらオブジェクトを生成
if(Input.GetKeyDown(KeyCode.Space))
{
Spawn();
}
}
// ランダムな位置にオブジェクトを作成する
void Spawn()
{
if (spawnObject == null) return;
if (weightedRandom == null) return;
// 各三角形の面積を考慮しつつランダムなインデックスを取得
int randomIndex = weightedRandom.GetRandomIndex();
int i1 = triangles[randomIndex * 3];
int i2 = triangles[randomIndex * 3 + 1];
int i3 = triangles[randomIndex * 3 + 2];
// 選択した三角形の内部にあるランダムな座標を計算
Vector3 p1 = vertices[i1];
Vector3 p2 = vertices[i2];
Vector3 p3 = vertices[i3];
Vector3 pos = RandomPointInsideTriangle(p1, p2, p3);
pos = transform.TransformPoint(pos);
// 選択した三角形の法線方向を計算
Vector3 n1 = normals[i1];
Vector3 n2 = normals[i2];
Vector3 n3 = normals[i3];
Vector3 normal = (n1 + n2 + n3).normalized;
normal = transform.TransformDirection(normal);
// 作成
Instantiate(spawnObject, pos, Quaternion.LookRotation(normal), transform);
}
// 三角形の内部にあるランダムな点を返す
Vector3 RandomPointInsideTriangle(Vector3 p1, Vector3 p2, Vector3 p3)
{
float a = Random.value;
float b = Random.value;
if (a + b > 1f)
{
a = 1f - a;
b = 1f - b;
}
float c = 1f - a - b;
return a * p1 + b * p2 + c * p3;
}
}
WeightedRandomクラスは前編で定義したとおりです。Start()であらかじめ三角形の面積計算や「重み」リストの登録など時間がかかる処理を終わらせておけば、Update()内でランダムな座標を計算してもそこまでパフォーマンスには影響を与えないはずです(もちろんInstantiateは連発すると少し重いですが…)。
70~78行目では、オブジェクトを生成する位置(pos)を計算するついでに三角形の面の向き(normal)も同時に算出し、オブジェクトの正面が外側を向くように調整しています。もし「面が下を向いている場合はオブジェクトを生成しない」というような条件をつけたい場合には、ここではじくのではなく、26~35行目あたりの三角形への重み付けをする段階であらかじめ条件に合わない三角形を外しておく(重みを 0 にしておく)のがいいと思います。
 |
| 「考えすぎた人」完成 |
そんなこんなで、メッシュ表面のランダムな座標を計算する方法については以上です!もっと簡単な別の方法があるかもしれませんが、とりあえずこういう方法もあるよ、ということで…
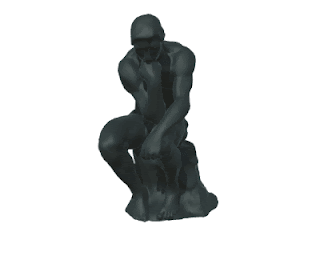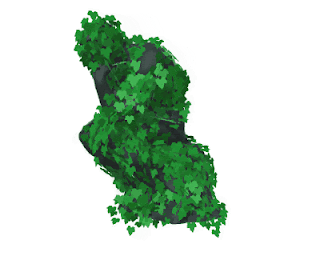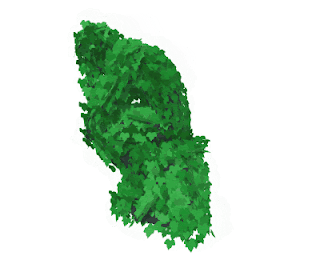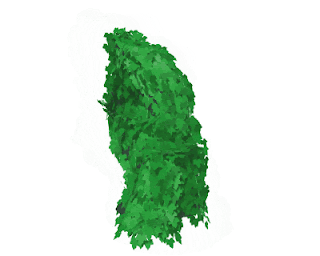
0 件のコメント:
コメントを投稿